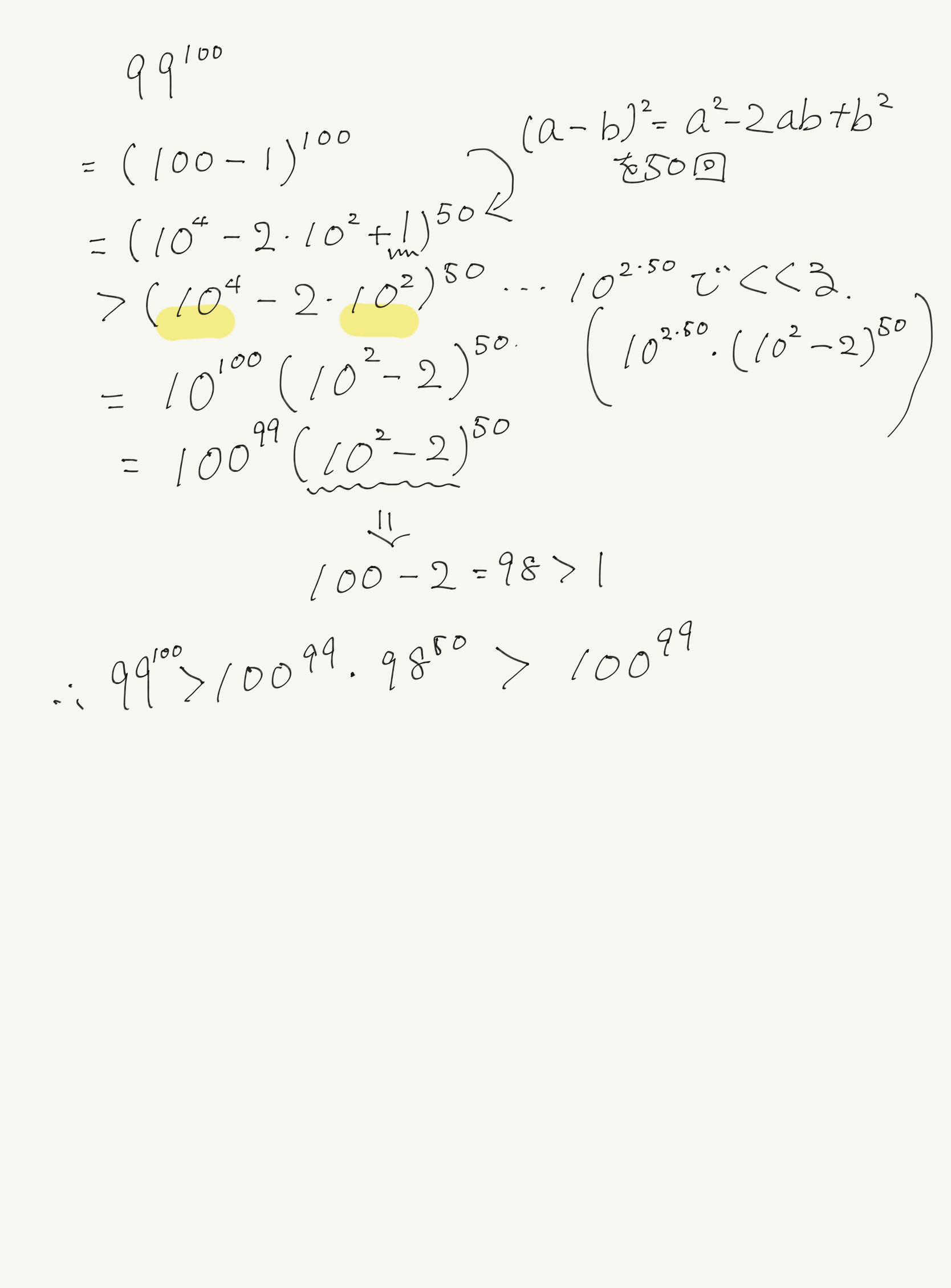こんにちは。さいどです。
今日、YouTubeを徘徊していたらこんな動画を発見。
数学の問題で、問題自体はいたってシンプル。
「99の100乗と100の99乗の大小を比較せよ」
理系の端くれとしてはこういう美しい問題に惹かれてしまいます。
脳で考えるより早く、ノートを気づいたら広げていました。
大きいべき数の問題は対数(log)を取れという受験生の嗅覚で色々こねくり回したのですが、さびついた頭ではどうにもならなかったので、泥臭く式変形した結果、多分うまくいったのでちょっとご紹介します。
間違ってたら知らせてください。
追記 案の定間違っていたとのご報告をいただきました。
直したものを載せます。正直、原型をとどめていないですが…
これも間違っていたら知らせてください。
訂正前の答案
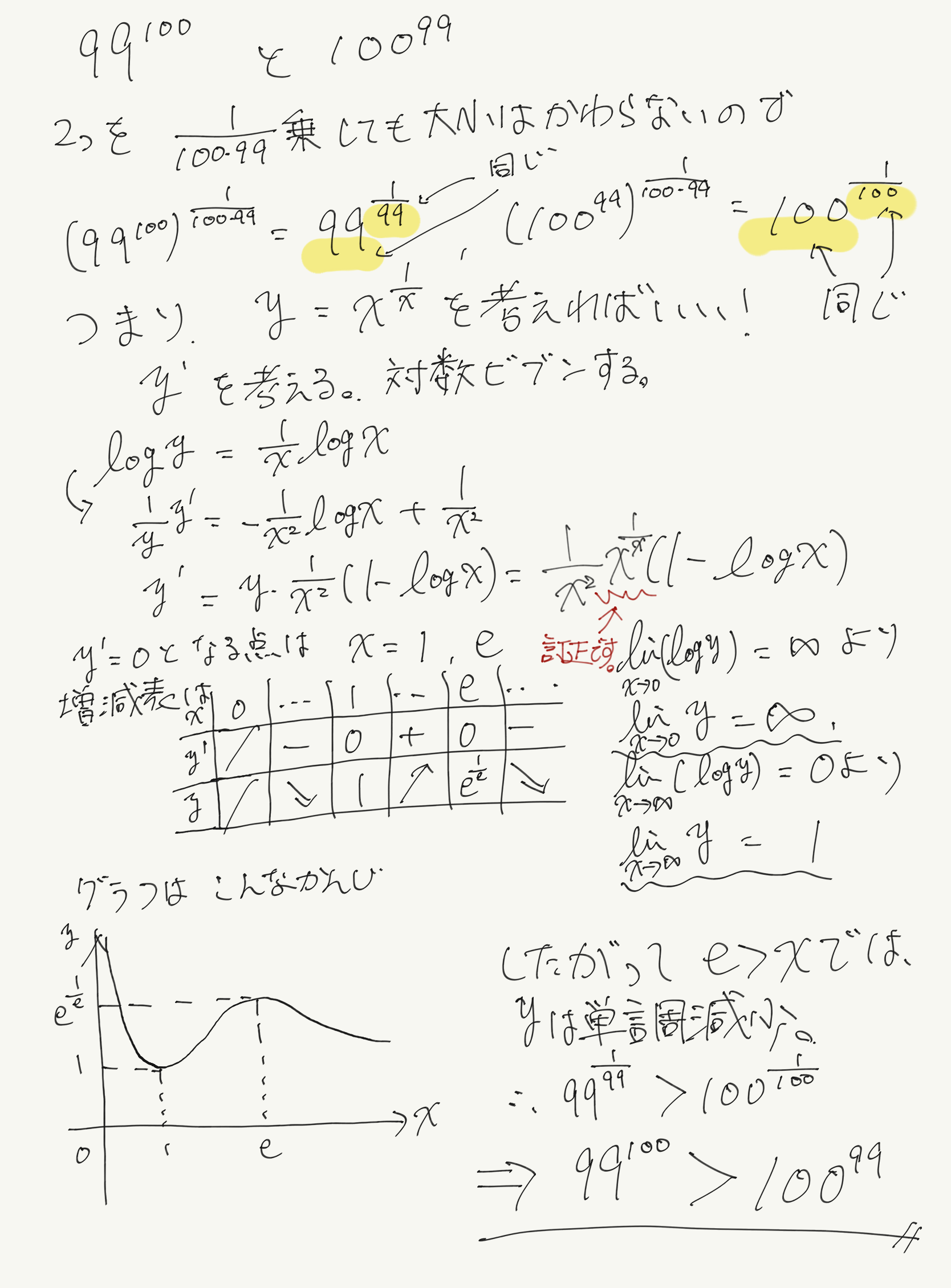
訂正後の答案

コンセプトは一行目に集約されていて、なんだか扱いにくい99を100ー1として、高1の序盤で習う二乗の展開の公式を使うだけです。
正直二行目の時点で100の99乗よりだいぶでかいのは明らかなのですが、大体きりの良いところまで変形してあげれば大小が求まりますね。
これで本番満点がもらえるかはかなり微妙ですが、医学部の問題を高1の知識だけで泥臭く解けちゃったりするんですよね。
ちなみに動画では数3の知識で微分して鮮やかに解いていたので、数3を習った方は動画の解説をぜひ見てみてください。

一応ときました。
追記 こっちも間違っていたので直しました。
こちらは訂正版に差し替えました。
もう脳みその劣化が著しい…
たまにこんな感じの受験数学を解いたりすると楽しいんですよね。
これ解いてみろよ!って問題やここがわかんないっていう問題がある方はぜひ送ってくださいね。(あんまり難しいのはダメです)できる限り頑張ります。
ではでは〜